Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Géométrie, Bleu, Rouge, Vert, Humour, Lapins, Formes animales dans les arts décoratifs, Formes -- Aspect symbolique, Jeux géométriques
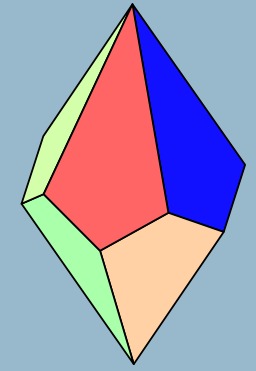
Comment dessiner un lapin
Comment dessiner un lapin avec Inkscape en utilisant trois formes et trois couleurs.
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Chiffres, Losanges, Dessin géométrique, As (cartes à jouer), Carreau (cartes à jouer), Carreaux (cartes à jouer)
As de carreau
Schéma d'un as de carreau. La carte ne présente ici aucune décoration particulière ; elle comporte deux index dans les coins supérieur gauche et inférieur droit, la valeur étant indiquée par "1".
Dessins et plans, Cartes à jouer, Jeux mathématiques, Rouge, Losanges, Dessin géométrique, As (cartes à jouer), Carreaux (cartes à jouer)
As de carreau
L'as de carreau a pour valeur l'as et pour enseigne le carreau. En abrégé, il est noté "1♦", plus rarement "A♦" comme ici. De façon générale, l'as de carreau peut être la plus forte carte des carreaux, suivant immédiatement le roi de carreau, ou la plus petite, précédant le deux de carreau. L'élément principal de la carte est un losange, situé en son centre, indiquant à la fois sa valeur et son enseigne. Source : http://fr.wikipedia.org/wiki/As_de_carreau
Photographie, Géométrie, Illusions d'optique, Art contemporain, Art optique, Art abstrait, Op art, Pécs (Hongrie), Victor Vasarely (1908-1997)
Composition monumentale de Vasarely en Hongrie
Œuvre de Vasarely (1908-1997) devant l'église Pálosok (Pálosok templom), rue János Hunyadi (Hunyadi János utca), à Pécs, en Hongrie. Op art, ou art optique, est une expression utilisée pour décrire certaines pratiques et recherches artistiques faites à partir des années 1960, et qui exploitent la faillibilité de l'œil à travers des illusions ou des jeux optiques. Les œuvres d'op art sont essentiellement abstraites. Les pièces donnent l'impression de mouvement, d'éclat de lumière et de vibration ou de mouvements alternés. Ces sollicitations visuelles placent le corps du spectateur en situation instable, entre plaisir et déplaisir, plongé dans une sensation de vertige proche de certains états d’ivresse légère. Ce phénomène est parfois renforcé par le caractère monumental des pièces, parfois des environnements, voire dans le cas d’art opticocinétique de réelles sources de lumière jaillissant de l’ombre. Source : http://fr.wikipedia.org/wiki/Op_Art
Dessins et plans, Calcul, Géométrie, Jeux mathématiques, Mathématiciens, Carrés magiques, John Horton Conway (1937-)
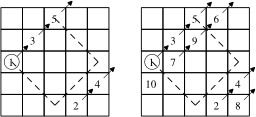
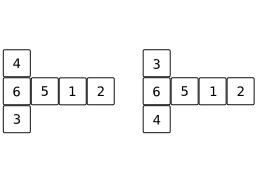
Construction d'un carré magique par la méthode du losange - 1
Premières étapes de la construction d'un carré magique 5x5 par la méthode du losange proposée par John Horton Conway : 1) Les nombres impairs 1, 3 et 5 sont inscrits selon une diagonale montante qui va de gauche à droite ; 2) Les nombres pairs 2 et 4 sont ensuite inscrits pour compléter la diagonale brisée ; 3) « Descendre » à la prochaine diagonale ; 4) Recommencer avec les nombres suivants.
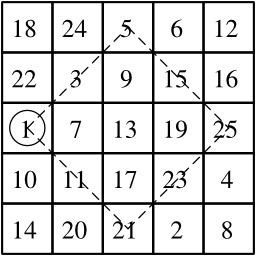
Construction d'un carré magique par la méthode du losange - 2
Un carré magique 5x5 construit selon la méthode du losange proposée par John Horton Conway : Le résultat final est un carré magique dont la constante est 65.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
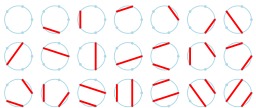
Cordes de Motzkin entre cinq points sur un cercle
Vingt-une cordes de Motzkin (qui ne se coupent pas) entre cinq points sur un cercle.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
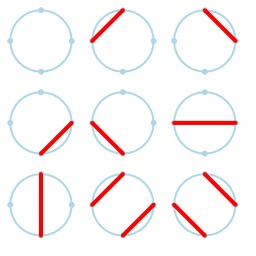
Cordes de Motzkin entre quatre points sur un cercle
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
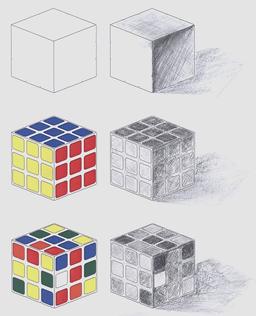
Cubes de rubik
Il s'agit d'un casse-tête géométrique à trois dimensions composé de 26 petits cubes (il n'y a pas de cube central) qui, à première vue, paraissent pouvoir se déplacer sur toutes les faces et ont l’air libres de toute attache sans tomber pour autant. Un système d’axes, dont le mécanisme a été breveté par son auteur, Ernő Rubik, se cache au centre du cube.
Dessins et plans, Géométrie, Jeux mathématiques, Jeux de logique, Mathématiciens, Devinettes et énigmes, Casse-tête logique, Énigmes mathématiques, Henry Dudeney (1857-1930)
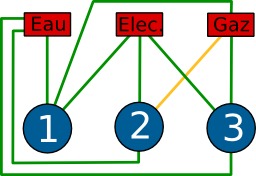
Enigme des 3 maisons
Enigme des trois maisons : Une solution généralement non admise dans l'énigme des trois maisons puisque les canalisations de gaz et d'électricité se croisent. Enigme posée en 1917 par Henry Dudeney (1857-1930) en ces termes : "Un lotissement de trois maisons doit être équipé d'eau, de gaz et d'électricité. La règlementation interdit de croiser les canalisations pour des raisons de sécurité. Comment faut-il faire ?"
Dessins et plans, Mécanique, Physique, Génie mécanique, Amortissement (mécanique), Analyse mécanique dynamique, Construction mécanique, Contact de roulement, Mécanique appliquée, Mécanique du contact
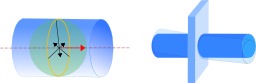
Force appliquée sous forme annulaire
Mécanique : force appliquée selon une forme annulaire. La modélisation des liaisons mécaniques s'appuie d'abord sur l'analyse de la géométrie de contact entre deux pièces. Dans un premier temps, lorsque les géométries sont considérées parfaites, on obtient un premier modèle présentant un certain nombre de degré de liaison ; ce modèle suppose un ajustement « glissant sans jeu », la liaison modélisée est dite « idéale ». Si l'on est en présence d'un jeu plus important, certains degrés de liaison disparaissent. Cela revient à considérer que les pièces flottent dans cet espace rendu disponible par le jeu. Si l'on veut modéliser correctement le comportement du système, il faut alors utiliser une autre liaison idéale que celle obtenue par l'analyse initiale. En particulier, pour avoir des machines performantes, il faut s'assurer que le mécanisme est conçu pour assurer aux pièces des positions exploitant ces jeux (alignements corrects). Ainsi, une liaison obtenue par emboîtement, sans jeu, deux cylindres complémentaires parfaits, constitue une liaison pivot glissant ; on parle de « centrage long ». Si on ajoute un jeu radial à cet ajustement, et qu'on diminue la longueur de portée, alors les deux cylindres peuvent se déplacer latéralement (mais cela reste imperceptible) et obliquer par rapport à la direction de l'axe. La liaison idéale qu'il faut utiliser pour modéliser l'assemblage est alors la liaison linéaire annulaire, et l'on parle de « centrage court ».
Photographie, Géométrie, Architecture des jardins, Architecture végétale des jardins, Podensac (Gironde. - région), Sauternes (Gironde), Vignobles, Géométrie de la ligne, Perspective
Jardin dans un vignoble
Photographie des jeux de ligne entre jardin et paysage du vignoble du Sauternais, entre minéral et végétal. Malle à Preignac-33.
Photographie, Géométrie, Couleurs, Jeux éducatifs, Jeux de dés, Jeux de société, Formes (mathématiques)
Jeu de formes géométriques
Jeu de plateau "Fits" : association de formes géométriques de couleur. Jeu créé par Charles B. Phillips et Ronald Wiecek en 1999 et édité par Ravensburger. Pour 2 à 4 joueurs, à partir de 8 ans, pour environ 5 à 15 minutes. Les joueurs cherchent à compléter une planche carrée à l'aide d'éléments géométriques de couleurs différentes le plus vite possible, tout en respectant des règles de placement relatives aux lignes de la planche et aux couleurs. Matériel : 4 planches de jeu, un support de pièces proposant 5 piles de pièces (2 pour chaque taille de triangle et 1 pour les carrés), 80 pièces de 4 couleurs différentes (rouge, jaune, vert et bleu) réparties de la manière suivante : 32 grands triangles, 32 petits triangles, 16 carrés ; et un dé spécial (2 faces "petit triangle", 2 faces "grand triangle", 1 face "carré" et 1 face "main").
Photographie, Géométrie, Jeux mathématiques, Jeux d'extérieur, Géants, Montréal (Canada), Tangram, Jeux de plein air
Jeux d'échecs et de tangram à Montréal
Réalisation de tangrams et jeux d'échecs géants, place Émilie-Gamelin, Montréal
Photographie, Géométrie, Échiquiers, Jeux mathématiques, Jeux d'extérieur, Montréal (Canada), Tangram, Jeux d'échecs, Jeux de plein air
Jeux de tangram de rue à Montréal
Jeux de tangram et jeux d'échecs en plein air, place Émilie-Gamelin, Montréal.
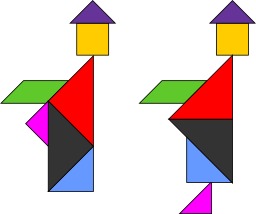
Le tangram des deux moines
Tangram du paradoxe des deux moines : même nombre de pièces mais disposées différemment.
Le tangram des trois vases
Le paradoxe du tangram magique des trois vases, par Sam Loyd, Eighth Book of Tan (1903).
Dessins et plans, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Mathématiques récréatives, Ferdinand Möbius (1790-1868), Collages (art)
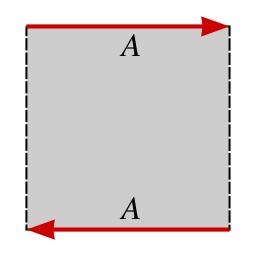
Montage d'un ruban de Möbius
Schéma de montage d'un ruban de Möbius : recoller les deux flèches en respectant le sens.
Dessins et plans, Géométrie, Jeux mathématiques, Pavages (mathématiques), Mathématiciens, Tuiles, Divertissements mathématiques
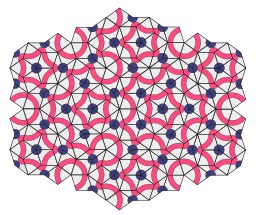
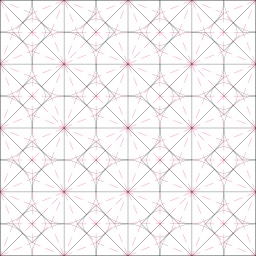
Pavage de Penrose avec tuiles apériodiques
Pavage de Penrose réalisé avec deux tuiles apériodiques. Roger Penrose est un mathématicien anglais. Les pavages de Penrose présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés). Ils ne sont pas périodiques, c'est-à-dire qu'on ne peut les décrire comme un motif répété sur une grille régulière. Ils sont cependant quasi-périodiques, c'est-à-dire que tout motif apparaissant dans le pavage réapparaît régulièrement. Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage. Les pavages de Penrose ne seraient restés qu'un joli divertissement mathématique si n'avaient été découverts, en 1984, des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux. Les pavages non périodiques, en particulier ceux de Penrose, s'avérèrent alors un modèle plausible de ces étranges matériaux. Cette découverte illustra à nouveau ce que Roger Penrose lui-même avait déjà remarqué en 1973, à propos d’un sujet de relativité générale : « On ne sait jamais vraiment quand on perd son temps ». Source : http://fr.wikipedia.org/wiki/Pavage_de_Penrose.
Dessins et plans, Géométrie, Jeux mathématiques, Oursins, Origami, Pliages en papier, Napperons individuels, Sets de table
Pliage de napperon en origami
Pliage de napperon en origami, à partir des recherches de J. Lang de pliages pour l'oursin. Source : http://en.wikipedia.org/wiki/Napkin_folding_problem
Dessins et plans, Géométrie, Cube, Jeux mathématiques, Origami, Pliages en papier, Racines numériques, Racines d'un nombre
Racine cubique de 2 et origami
Doubler le volume d'un cube : PB/PA = racine cubique de 2. Comment construire la racine cubique de 2 par pliage d'origami : construction par Peter Messer, Problème 1054, Crux Mathematicorum, Vol. 12, No. 10, 1986, pp. 284-285.
Dessins et plans, Nombres cardinaux, Chiffres, Imagerie (psychologie), Images mentales, Jeux arithmétiques, Géométrie des nombres
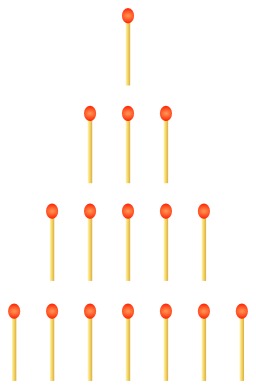
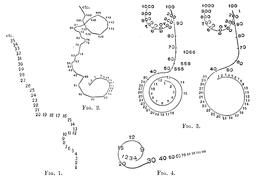
Représentations linéaires de nombres
Plusieurs exemples de représentations linéaires de nombres, 1892-1893. Source : Popular Science Monthly, Volume 42, "Number forms", par G. T. W. Patrick, professeur de philosophie à l'université d'Iowa.
Photographie, Géométrie, Jeux mathématiques, Rubans, Ruban adhésif, Pliages en papier, Mathématiques récréatives, Ferdinand Möbius (1790-1868)
Ruban de Moebius
Ruban de Moebius construit à partir d'une bande de papier, un ruban adhésif retenant les deux bouts. Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités. En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou boucle de Möbius) est une surface compacte dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Source : http://fr.wikipedia.org/wiki/Ruban_de_M%C3%B6bius.
Photographie, Géométrie, Boîtes à jeux, Engrenages en plastique, Jeux et récréations, Loisirs créatifs, Spirographes
Spirographe
Instrument de loisir créatif. Le Spirographe, marque déposée par Hasbro, est un instrument de dessin permettant de tracer des figures géométriques, des courbes mathématiques techniquement connues sous le nom d'hypotrochoïdes. Le Spirographe a été inventé par Denys Fisher, qui l'a présenté en 1965 au Salon du jouet de Nuremberg. Les droits de distribution ont été acquis par Kenner, qui l'introduit sur le marché américain en 1966. Le Spirographe est composé de différentes roues et d'anneaux dentés en plastique transparent. Les roues sont les pièces mobiles, et se positionnent dans les anneaux, pièces fixes, de manière à pouvoir y tourner grâce au système d'engrenages.
Dessins et plans, Géométrie, Carré, Jeux mathématiques, Origami, Pliages en papier, Théorèmes -- Démonstration automatique, Mathématiques japonaises, Nombres rationnels
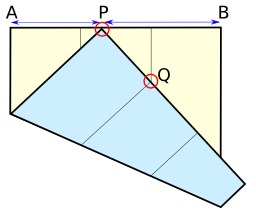
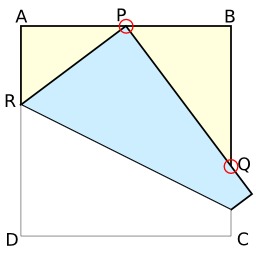
Théorème de Haga et origami
Théorème de Haga et origami : BQ est rationnel si AP l'est, par pliage du sommet d'un carré sur un point P du côté opposé. Source : http://en.wikipedia.org/wiki/Mathematics_of_origami.
Trapézoèdre pentagonal
Trapézoèdre pentagonal : 10 faces en cerf-volant - dual : antiprisme pentagonal. Le trapézoèdre pentagonal est le premier solide différent des solides de Platon utilisé comme un dé dans les jeux de rôle tels que Donjons et Dragons. Ayant 10 côtés, il peut être utilisé en répétition pour générer n'importe quelle probabilité discrète désirée de base décimale.
Dessins et plans, Géométrie, Jeux mathématiques, Origami, Pliages en papier, Résolution de problème, Trisection de l'angle
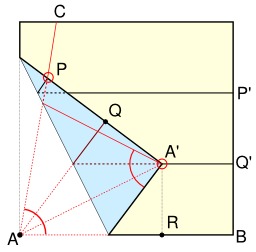
Trisection d'un angle et origami
Trisection de l'angle CAB : résolution d'un problème ne pouvant se faire par la méthode traditionnelle "à la règle et au compas".